Efecto Doppler:
El efecto Doppler, llamado así por el físico austríaco Christian Andreas Doppler, es el aparente cambio de frecuencia de una onda producido por el movimiento relativo de la fuente respecto a su observador. Doppler propuso este efecto en 1842 en su tratado Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (Sobre el color de la luz en estrellas binarias y otros astros).
El científico neerlandés Christoph Hendrik Diederik Buys Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y confirmó que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como "efecto Doppler-Fizeau" y en los Países Bajos como el "efecto Doppler-Gestirne".
En el caso del espectro visible de la radiación electromagnética, si el objeto se aleja, su luz se desplaza a longitudes de onda más largas, desplazándose hacia el rojo. Si el objeto se acerca, su luz presenta una longitud de onda más corta, desplazándose hacia el azul. Esta desviación hacia el rojo o el azul es muy leve incluso para velocidades elevadas, como las velocidades relativas entre estrellas o entre galaxias, y el ojo humano no puede captarlo, solamente medirlo indirectamente utilizando instrumentos de precisión como espectrómetros. Si el objeto emisor se moviera a fracciones significativas de la velocidad de la luz, sí sería apreciable de forma directa la variación de longitud de onda.
Sin embargo, hay ejemplos cotidianos del efecto Doppler en los que la velocidad a la que se mueve el objeto que emite las ondas es comparable a la velocidad de propagación de esas ondas. La velocidad de una ambulancia (50 km/h) puede parecer insignificante respecto a la velocidad del sonido al nivel del mar (unos 1.235 km/h), sin embargo, se trata de aproximadamente un 4% de la velocidad del sonido, fracción suficientemente grande como para provocar que se aprecie claramente el cambio del sonido de la sirena desde un tono más agudo a uno más grave, justo en el momento en que el vehículo pasa al lado del observador.
Observador acercándose a una fuente
Imaginemos que un observador O se mueve con una velocidad  que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad
que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad  , frecuencia
, frecuencia  y longitud de onda
y longitud de onda 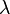 . Por lo tanto, la velocidad de las ondas respecto del observador no será
. Por lo tanto, la velocidad de las ondas respecto del observador no será  , sino la siguiente:
, sino la siguiente:
 que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad
que tiene una dirección y sentido hacia una fuente de sonido S que se encuentra en reposo. El medio es aire y también se encuentra en reposo. La fuente emite un sonido de velocidad  , frecuencia
, frecuencia  y longitud de onda
y longitud de onda 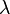 . Por lo tanto, la velocidad de las ondas respecto del observador no será
. Por lo tanto, la velocidad de las ondas respecto del observador no será  , sino la siguiente:
, sino la siguiente:
Sin embargo, no debemos olvidar que como la velocidad del medio no cambia, la longitud de onda será la misma, por lo tanto, si:

Pero como mencionamos en la primera explicación, el observador al acercarse a la fuente oirá un sonido más agudo, esto implica que su frecuencia es mayor. A esta frecuencia mayor captada por el observador se la denomina frecuencia aparente, que la denominamos  .
.
 .
.
El observador escuchará un sonido de mayor frecuencia debido a que 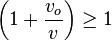
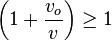
Ejemplo;
Un observador se mueve a una velocidad de 42 m/s hacia un trompetista en reposo. El trompetista está tocando (emitiendo) la nota La (440 Hz). ¿Qué frecuencia percibirá el observador, sabiendo que  = 340 m/s
= 340 m/s
 = 340 m/s
= 340 m/s
Solución: Si el observador se acerca hacia la fuente, implica que la velocidad con que percibirá cada frente de onda será mayor, por lo tanto la frecuencia aparente será mayor a la real (en reposo). Para que esto ocurra debemos aplicar el signo (+) en la ecuación.


En este caso particular, el trompetista emite la nota La a 440 Hz; sin embargo, el observador percibe una nota que vibra a una frecuencia de 494,353 Hz, que se aproxima altamente a la frecuencia perteneciente a la nota Si. Musicalmente hablando, el observador percibe el sonido con un tono más agudo del que se emite realmente.
¿Qué sucede con los receptores respecto a la frecuencia con que perciben el sonido de la moto?
Veamos:
Todo depende de las velocidades de los involucrados.
La chica de la izquierda está en reposo, respecto a ella, el sonido debería llegar a la velocidad de 343 m/s, pero resulta que el emisor del sonido (la moto) se aleja de ella a 22 m/s; por lo tanto, a ella le llega el sonido solo a 321 m/s (343 menos 22), por lo tanto percibirá un sonido de menor frecuencia (ondas más largas, tono menos agudo).
El muchacho de la derecha camina, supongamos a 3 m/s, hacia la moto. Respecto a este muchacho, el sonido viaja hacia él a 343 m/s, más los 22 m/s de la moto y más los 3 m/s de su caminar hacia la moto; por lo tanto, percibirá un sonido de mayor frecuencia, ondas más cortas, tono más agudo).
Entendida esta relación entre las velocidades, ahora mostraremos cómo es posible obtener ecuaciones que nos permiten calcular las variaciones de frecuencia percibidas por un receptor.
Para no complicar vuestra existencia estudiantil estableceremos que la siguiente fórmula general permite hallar la frecuencia que percibirá el receptor u observador:
Donde :
fo = frecuencia que percibe el observador (también se usa como fr o frecuencia de la señal recibida)
ff = frecuencia real que emite la fuente (también se usa como fe o frecuencia de la señal emitida)
vs = velocidad del sonido (343 m/s)
vo = velocidad del observador (también se usa como vr o velocidad del receptor)
vf = velocidad de la fuente (también se usa como ve o velocidad del emisor)
Debemos fijar la atención en los signos + (más) y – (menos) de la ecuación. Notemos que en el numerador aparece como ± (más menos) y en el denominador aparece invertido (menos más). Esta ubicación de signos es muy importante ya que usar uno u otro depende de si el observador se acerca o se aleja de la fuente emisora de sonido.
Importante:
Si el observador se acerca a la fuente emisora, el signo en el numerador será + (más) y simultáneamente el signo en el denominador será – (menos).
Ahora, si el observador se aleja de la fuente emisora, el signo en el numerador será – (menos) y simultáneamente el signo del denominador será + (más).
La radio emite un sonido con frecuencia de 440 Hz
El mono (perdón, el receptor u observador) camina hacia la fuente (la radio, fija) con velocidad de 20 m/s
Pregunta: ¿con qué frecuencia recibe el sonido el receptor?
Analicemos los datos que tenemos:
fo = x (desconocida): frecuencia que percibe el observador
ff = 440 Hz: frecuencia real que emite la fuente
vs = 343 m/s: velocidad del sonido
vo = 20 m/s: velocidad del observador (con signo + ya que se acerca a la fuente)
vf = 0: velocidad de la fuente (fuente en reposo)
Usemos nuestra fórmula y coloquemos los valores:
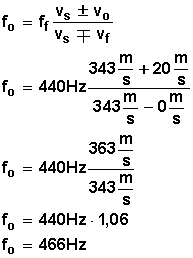
Nótese que la velocidad de la fuente (la radio) es 0 (cero) pues se haya en un lugar fijo, no tiene movimiento.
Respuesta:
El receptor (el mono) percibe el sonido con una frecuencia de 466 Hz.
La clave para resolver este y otros ejercicios está en saber colocar el signo de suma o de resta a la velocidad del receptor y la del emisor.
Ejemplo:
La sirena de la ambulancia emite un sonido cuya frecuencia es 200 Hz.
La ambulancia viaja a 80 m/s (alejándose del receptor)
El receptor (el mono) se aleja de la ambulancia a velocidad de 5 m/s (con signo – pues se aleja de la fuente)
Pregunta: ¿con qué frecuencia recibe el sonido el receptor?
Hacemos lo mismo del ejemplo anterior, usamos la fórmula y ponemos los valores:
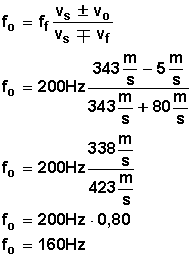
Respuesta:
El receptor (el mono) percibe el sonido con una frecuencia de 160 Hz.




No hay comentarios:
Publicar un comentario